The proposed concept has significant practical applications in the pharmaceutical industry, as it would allow medicines and active fluids to be stored for long periods of time using such containers and eliminate concerns related to sedimentation. Although additional research and development are required to arrive at a practical, optimized, commercial design, this preliminary work outlines the mathematical development and computational verification of the concept.
Sedimentation and Marangoni Forces
During gravitational settling of particles, a definitive vertical concentration gradient gradually develops. Undesired sedimentation occurs in unstable colloidal dispersions, which can then form loosely joined masses of fine particles of either aggregates or agglomerates (due to interparticle attractions) as the particles assemble. Although aggregation is a reversible process, agglomeration is not. Both should be avoided if possible.
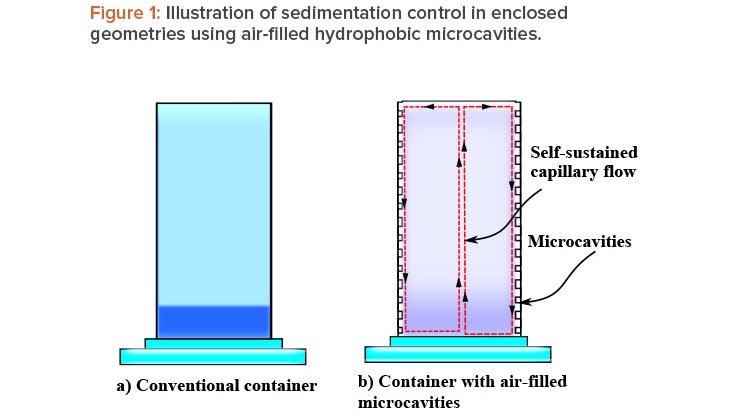
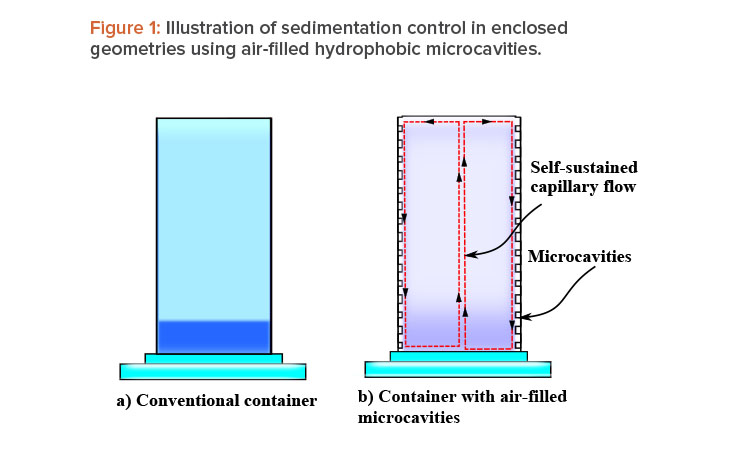
If the walls of a container are lined with air-filled (or inert gas–filled) hydrophobic microcavities, a Marangoni force will appear because of the dependence of surface tension on concentration. This Marangoni force will propel the particles from the low-
surface-tension region to the high-surface-tension region. The force will then act as a negative feedback and prevent sedimentation, agglomeration, and aggregation of particles by mildly, yet continuously, remixing the content.
The use of walls lined with air-filled hydrophobic microcavities and superhydrophobic surfaces is not new; however, its application has so far been limited to being a passive method for drag reduction in which the air-liquid interface, owing to the trapped air of the nanocavity, translates into the appearance of slip velocity in the superhydrophobic surface. Active research in this topic encompasses science and technology to understand, mitigate, or prevent the phenomena., , , , , , This article provides a first assessment for a passive and self-sustained mechanism able to prevent gravitational settling, agglomeration, and cluster formation in enclosed geometries by using walls lined with air-filled hydrophobic microcavities. This concept has direct relevance to pharmaceutical engineering, as sedimentation and agglomeration issues play a very important role in the pharmaceutical industry.
Self-Sustained Sedimentation Control
The Marangoni effect is the mass transfer along an interface between two fluids due to a gradient of the surface tension. In the case of temperature dependence, this phenomenon is generally referred as thermocapillary convection.,
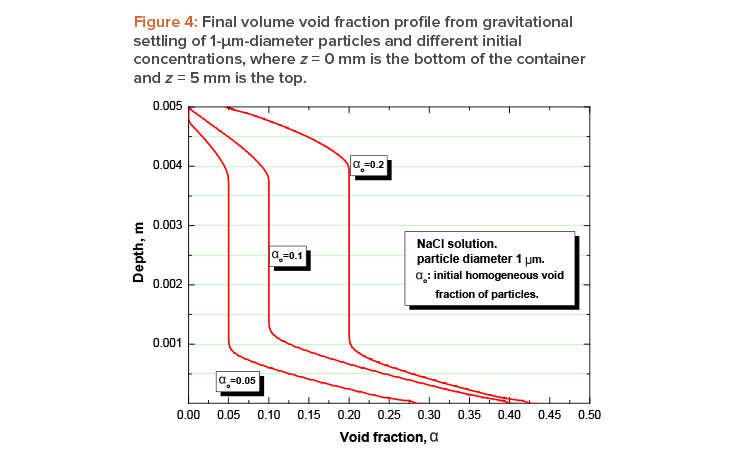
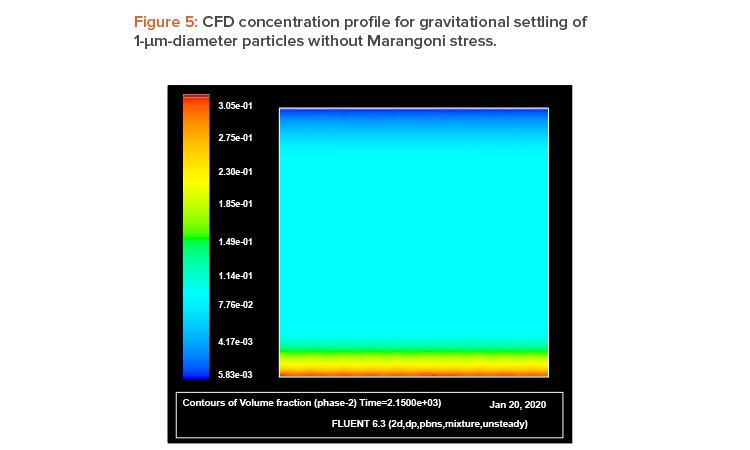
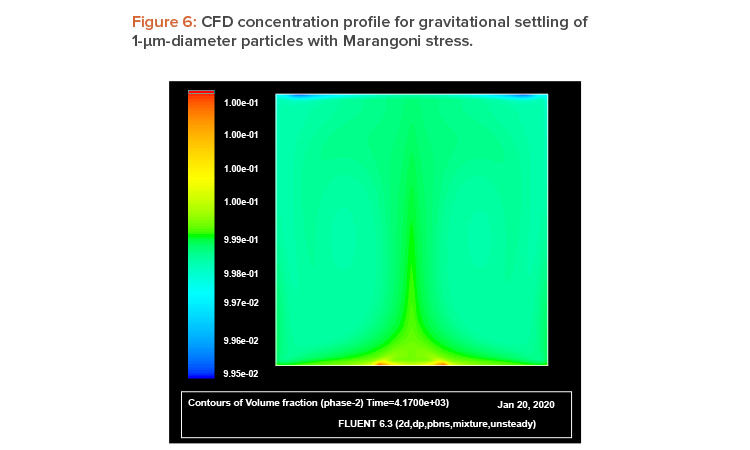
The explanation of this phenomena is straightforward: A liquid with a high surface tension pulls more strongly on the surrounding liquid than one with a low surface tension, and therefore the presence of a gradient in surface tension will naturally cause the liquid to flow away from low-surface-tension regions toward high-surface-tension regions. The surface tension gradient can be created by a thermal gradient, owing to its temperature dependence, or by a concentration gradient. The concentration dependence provides the possibility to use walls lined with air-filled (or inert gas–filled) hydrophobic microcavities as a self-controlled and completely passive method to prevent sedimentation, agglomeration, and cluster formation in enclosed geometries. As mentioned, during gravitational settling, a vertical concentration gradient starts to develop, with the higher concentration at the bottom (sedimentation). Thus, if container walls are lined with such microcavities, the concentration gradient can trigger a capillary motion that will act as a feedback, preventing or mitigating the sedimentation process. As the concentration gradient (sedimentation rate) increases, the capillary flow becomes stronger. (Figure 1 illustrates this idea.)
Methods
First, consider a fully developed, two-dimensional flow between parallel plates that are separated by a distance, b, and a length, h, and lined with air-filled hydrophobic microcavities. When precipitation and gravitational settling start, a vertical concentration gradient appears and, as a result, a Marangoni stress is generated across the wall because of the free interfaces introduced by the microcavities (as described previously). The maximum velocity, vmax, attainable by this Marangoni flow—which might be used as a rough estimation of the capability for resuspension of particles—occurs at the wall, and can be estimated using the following equation:
Equation 1: Vmax≈b2μdσdz
where b is the distance between plates, μ is the dynamic viscosity of the liquid, and dσ/dz is the surface tension gradient. In our case, because the surface tension gradient is driven by a concentration gradient,∇ZC, equation 1 can be rewritten as follows:
Equation 2: Vmax≈bσc2μ∇zC
where σc is the surface tension coefficient with concentration.
Finally, the feasibility for resuspension of sediment by the induced capillary flow may be preliminarily assessed by equating equation 2 with the terminal velocity of particles, which, for a low Reynolds number less than unity, is calculated as follows:
Equation 3: Vt=g(d2p)18μ(ρρ−ρ)
where g is gravity, dp is the diameter of the particle of solute, μ is the dynamic viscosity of the fluid, and ρρ and ρ are the density of the particle and the density of the fluid, respectively. Equating equation 2 with equation 3, we obtain:
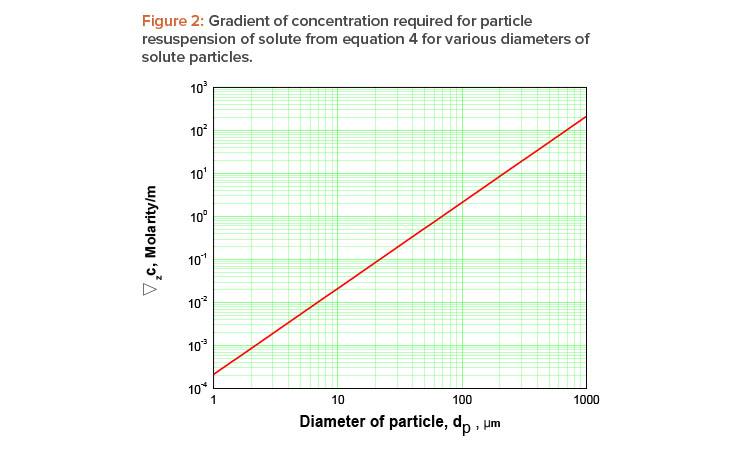
Equation 4: ∇zC=gd2p9σcb
which gives us the concentration gradient required to compensate the gravitational settling as a function of the diameter of the particle.
Looking at equation 4, one may think that the required concentration is reduced inasmuch that the distance between plates, b, increases. However, this is not the case because equation 2 for the capillary velocity cannot be used for any size of container. Further, in the derivation of equation 2 in the momentum equations, it was assumed that
Vz2h<<μ|vz|ρb2
and then the validity of the velocity flow by equation 2 is given by:
Equation 5: b2<<4μ2ρh|σc|∇zC
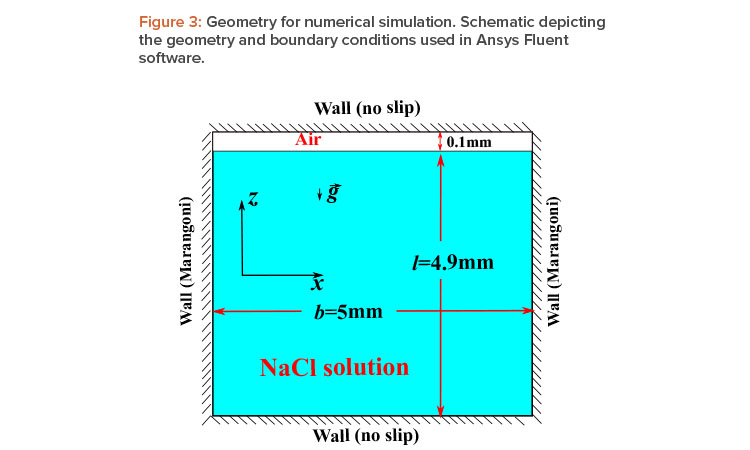
To obtain some idea of the concentration gradient predicted by equation 4, let us assume some typical values for a NaCl
solution with densities ∇ ≈ 103 kg/m3 and ∇p ≈ 2.17 × 103 kg/m3; μ ≈ 10–3 Pas; ∇c = 1.2 × 10–3N/m(molarity); and a distance between plates b = 5 mm, compatible with the requirement given by equation 5.